Logikgatter und Wahrheitstabellen

Typen von Logikgattern und Symbolik (Wikipedia)

Name

Funktion

Symbol in Schaltplan

Wahrheits-
tabelle

IEC 60617-12 : 1997 &
ANSI/IEEE Std 91/91a-1991

ANSI/IEEE Std 91/91a-1991

DIN 40700 (vor 1976)

Und-Gatter
(AND)

Y = A \wedge B

Y = A\cdot B

Y = A\,B

Y = A\,\&\,B

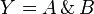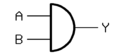Oder-Gatter
(OR)

Y = A \vee B

Y = A + B\,

Nicht-Gatter
(NOT)

Y = \overline{A}

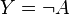Y = \neg A

Y = \tilde A

A	Y
0	1
1	0

NAND-Gatter (NICHT UND)
(NOT AND)

Y = \overline{A \wedge B}

Y = A \overline{\wedge} B

Y = \overline{A\,B}

Y = A|B

NOR-Gatter (NICHT ODER)
(NOT OR)

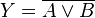Y = \overline{A \vee B}

Y = A \overline{\vee} B

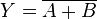Y = \overline{A + B}

Y = A - B

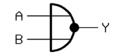XOR-Gatter (Exklusiv-ODER, Antivalenz)
(EXCLUSIVE OR)

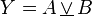Y = A \,\underline{\lor}\, B

Y = A \oplus B

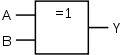oder

XNOR-Gatter (Nicht-Exklusiv-ODER, Äquivalenz)
(EXCLUSIVE NOT OR)

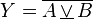Y = \overline{A \,\underline{\lor}\, B}

Y = A \,\overline{\underline{\lor}}\, B

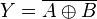Y = \overline{A \oplus B}

Y = A \odot B

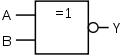oder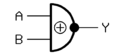

Mehr zu Logikgattern und Wahrheitstabellen (Wikipedia):